【ψ3～4】二つの空間の概要―4次元空間（ψ3）と4次元時空（ψ4）

▼ 参考文献 ▼

ψ1～2のおさらい

まずは、ψ1～2のおさらいから入りたいと思います。

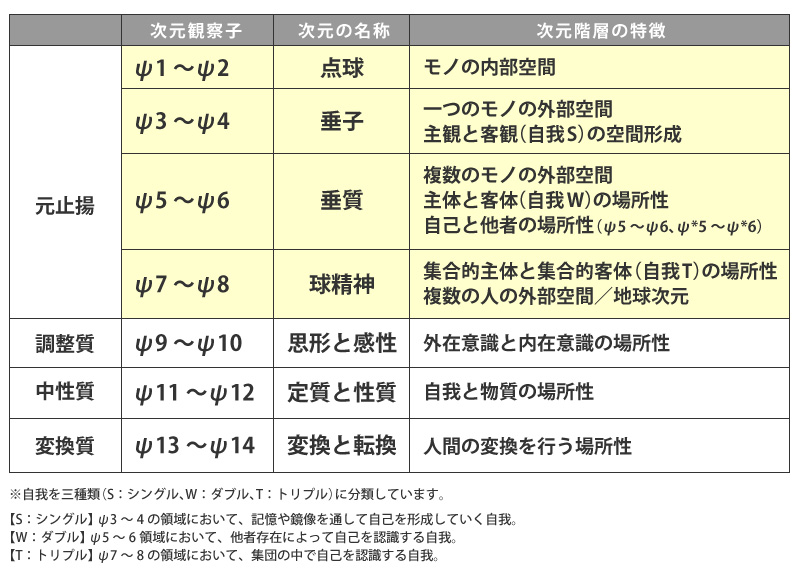
次元観察子ψ1～2は下記の通りです。

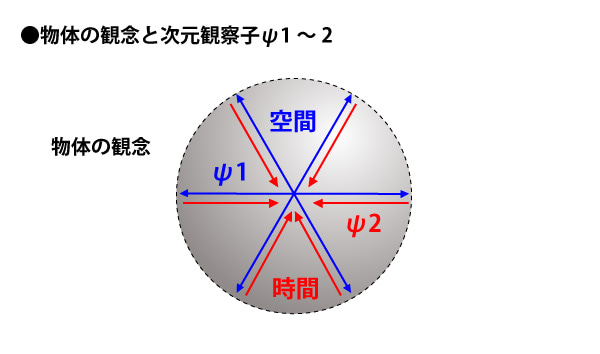
この領域で、私たち人間の「時空」に対する観念が生まれています。

そして、この領域が次元上昇することで、次なる領域ψ3～4が出現してきます。

ψ3～4の空間について

ψ3～4の空間を、簡潔にお話すると下記のような特徴があります。

ψ3：ψ1～2を等化した次元

さらに、それぞれの観察子がどのような空間の特徴を持っているかというと、まずψ3は「ψ1：空間」と「ψ2：時間」を等化した次元になります。

「等化」については、これまでも何度か触れてきましたが、簡単におさらいすると

対化同士を等しいものにする

という、宇宙の精神の力（ヌースの力）のことをいいます。

よってψ3は、「ψ1：空間」と「ψ2：時間」を等しくした空間になるため、

「ψ3：空間＝時間」となり、言い換えると、

ψ3：時間が空間化した世界

になります。

次元的に表現すると、「4次元空間」になるかと思います。

この「時間が空間化した世界」については次回以降詳しくお話していきますが、イメージとしては映画のフィルムのような世界です。

空間と時間がセットになっている、そんな世界です。

ψ4：ψ3が中和した次元

そしてψ4の空間は、ψ3の反映として出現してくる世界になります。

「反映」とはわかりやすく説明すると、

下次元の観察子の対化を等化できなかった

ことをいいます。

今回の件だと、「ψ1：空間」と「ψ2：時間」を等化できなかったということは、「ψ4：空間≠時間」となり、これを言い換えると、

ψ4：空間が時間化した世界

という形になります。

次元的に表現すると、「時空4次元（時空4次元連続体）」になるかと思います。

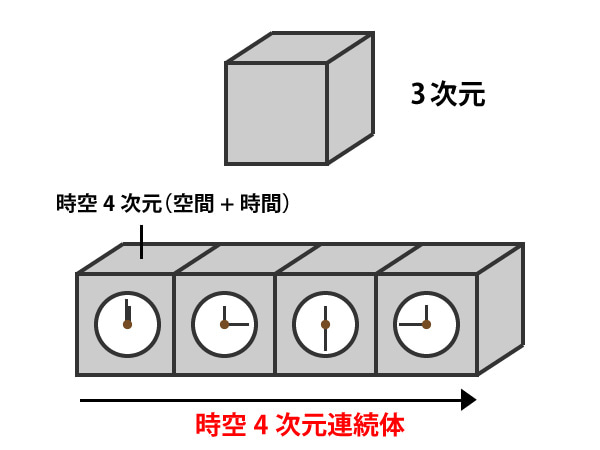
「空間が時間化した世界」とは、空間と時間がセットにならず、一つの空間内で時間だけが流れているように感じる世界です。

それは、今まさに私たちが見ている世界そのもののことです。

ψ3～4における膨張と収縮

収縮したψ3、膨張したψ4

私たちは意識が転倒しているので、偶数側の空間しか見られないようになっていますが、奇数側の空間は一体どこにいってしまったのでしょうか？

じつは、ψ4の空間が顕在化しているとき、ψ3の空間はミクロレベルにまで収縮してしまっています。

この収縮という動きは、あのψ1～2の「膨張・収縮」の動きが、そのまま上次元に引き継がれている、と考えてみてください。

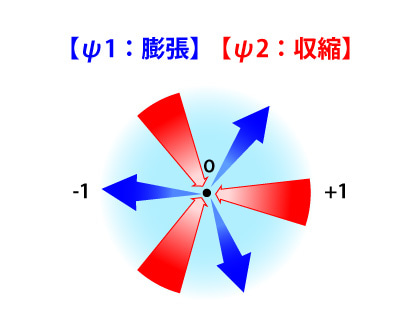
ψ4が顕在化しているということは、ψ4の空間が「膨張」して出現しているということです。

その際、ψ3の空間は逆に「収縮」してしまっています。

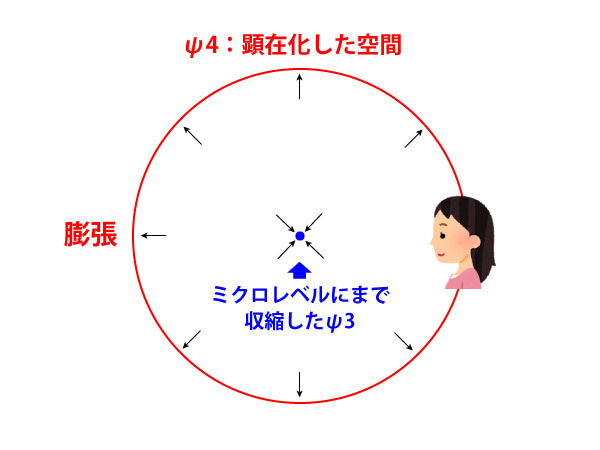
ψ3の世界は消えてなくなったわけではないので、ψ4の意識状態において、ミクロレベルにまで観察の範囲を広げると

ようやく素粒子世界にψ3を見つけることができる

というわけです。

膨張したψ3、収縮したψ4

そして、上記の逆パターンもあります。

ψ3が顕在化した場合、今度はψ3が膨張して出現するので、ψ4の方が収縮します。

書籍『2013：シリウス革命』の中で、OCOTが私たちが見ている世界のことを、

と発言する場面があります。

それは、OCOTたちの意識は奇数側の空間が顕在化しているので、偶数側の空間がミクロレベルにまで収縮してしまっているので、そのような発言になるのかなと考えました。

まとめ

ちなみに本家ヌーソロジーでは、ψ3とψ4を下記のように表現します。

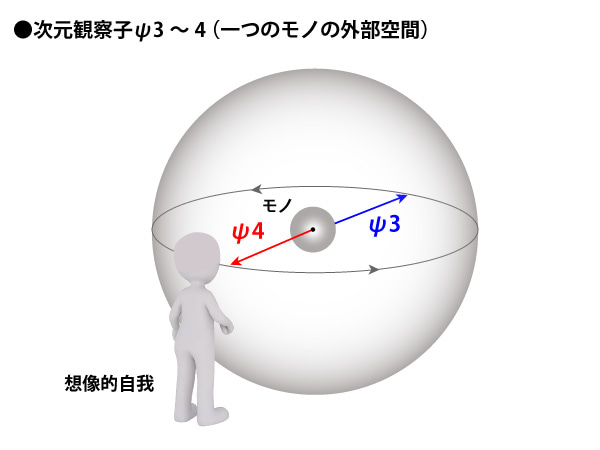
おっと、なんだか不思議な球空間ですね！

なぜこのようにψ3とψ4を分けているのでしょうか？

図を見たまま表現すると、それぞれの観察子の矢印の方向は、モノを中心にψ3は「前」、ψ4は「後ろ」になっていますね。

それぞれの観察子の特徴を理解するためには、「主体と客体」「前と後ろ」の概念について学ぶ必要があります。

というわけで、次回以降はψ3とψ4の違いについて詳しくお話をしていきたいと思います。

次回もお楽しみに♪

▼ 参考文献 ▼