私の宇宙からこんにちは、natanです。
今日はヌーソロジーの三種の神器の一つである、ケイブコンパスについて解説したいと思います。
以下の解説は、本家ヌーソロジーの内容を私流に解釈したものです。本家ヌーソロジーの解説とは異なりますので、ご理解のほどよろしくお願いします。
ケイブコンパスとは?
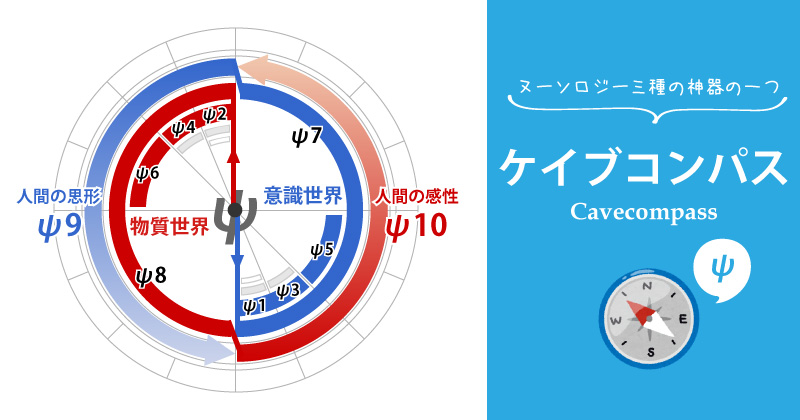
「ケイブコンパス」とは、ケイブユニバースの中で流動している、ヌースとノスが持ったさまざまな次元の方位を、正確に捉えるための羅針盤のようなものです。
観察子構造の中では、観察子が双対的に関係性のネットワークを張り巡らせています。
人間の意識の中では、知覚や言語、記憶などを通じて思考や感情、意志などが複雑に絡み合いながらさまざまな活動を行っています。
これらの活動の様子を正しく見定めていくために、ケイブコンパスが役に立つのです。
では早速、ケイブコンパスを詳しく見ていきます。
natan流ケイブコンパスの解説
前回のおさらい
前回のおさらいを少し挟みます。
私たちの意識は、高次の脈性観察子Φ7~14が凝縮化&反転することで、次元観察子ψ1~8に入り込んでいるとお話しました。
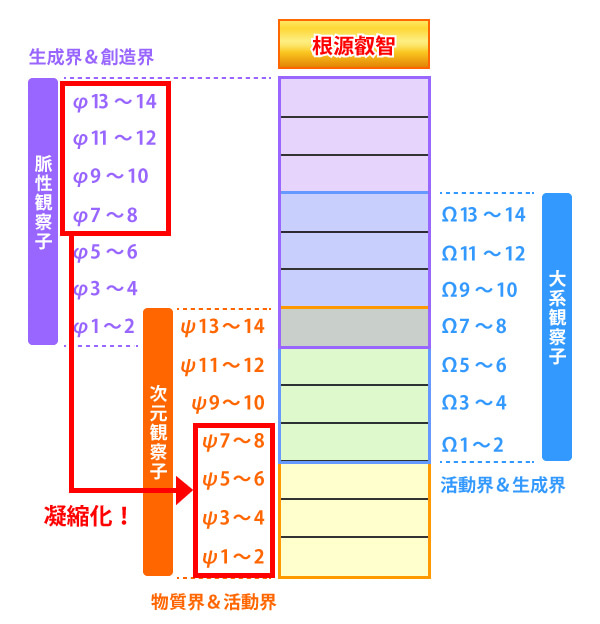
そのため、偶数先手(ノス先手)の意識活動が起こっているとご紹介しました。
なので、本来はケイブコンパスもヌース先手で動くはずだったものが、反転することで、ノス先手で動くようになっています。
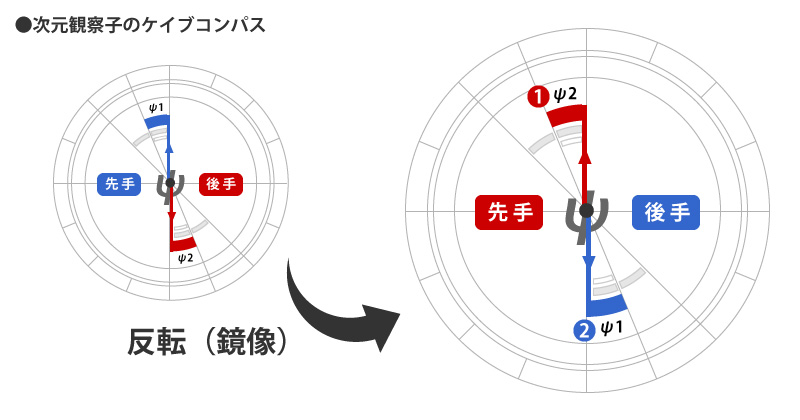
ケイブコンパスの動き方(ψ2~4、ψ1~3)
ケイブコンパスはその名の通り「コンパス」ですので、中心部分からヌースとノスの力が出てきて、少しずつ半円を描くように進んでいきます。
この状態に意識活動を当てはめてみると、下記のようなイメージになります。
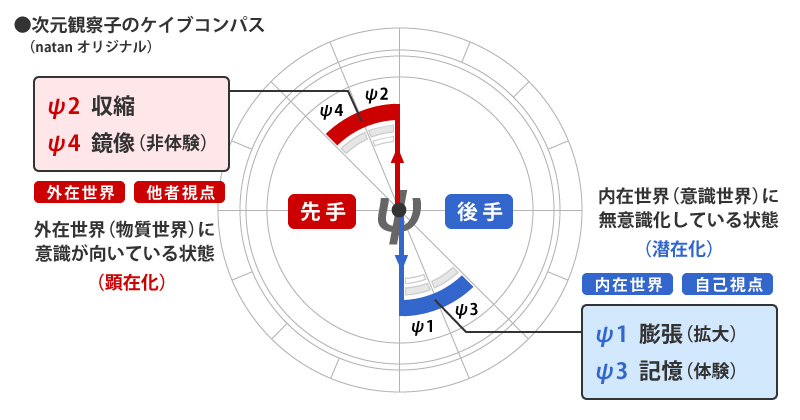
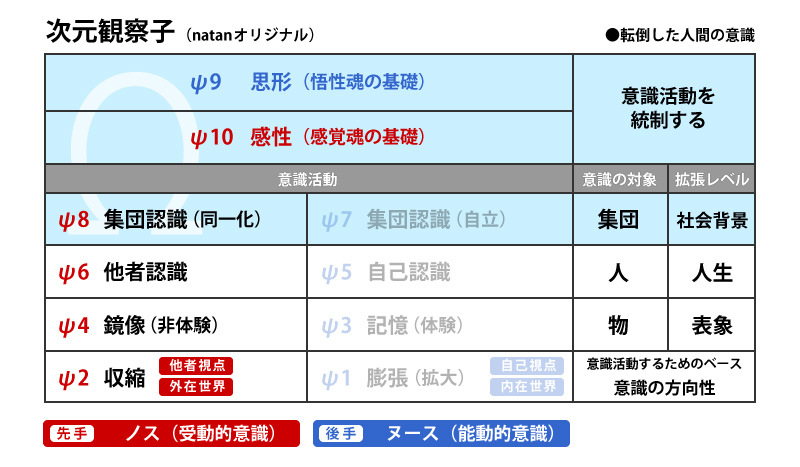
人間の意識は偶数系のノス先手で動くので、強制的に物質世界、もしくは他者側に意識が向くようになっています。
物質世界に意識が向いていることは言い換えれば、「起きている状態」とも取れるので、その意識状態を「顕在意識」として見ることもできます。
また、奇数系のヌース側は後手に回っているので、偶数系のノスの後に動きます。
「ノスを経験した後、ヌースとして自己を省みる」という意味合いで、ヌースが後手で動くと捉えるとわかりやすいかな?
偶数系のノスが「顕在意識」ならば、その逆で奇数系のヌース側は「無意識」として見ることができます。
ψ6~ψ5
さらにケイブコンパスの針を進めます。
ψ6~5はこのような感じです。
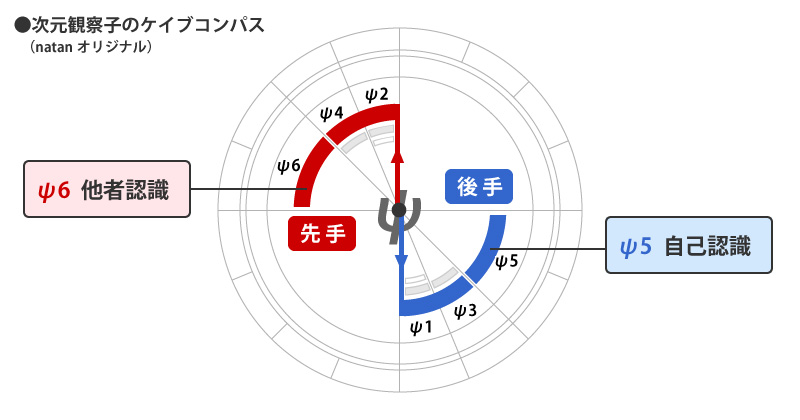
「ψ6:他者認識」が先行し、後手で「ψ5:自己認識」が動きます。
この状態を、実生活に置き換えて考えてみると、「他者軸で動くことによって、そこでつらさや苦しさを経験し、自己の行動を顧みて、自分軸で動くよう気持ちを切り替える」みたいに思っていただければわかりやすいかと。
ψ8~7
そしてさらに針は進み、ψ8~7はこんな感じです。
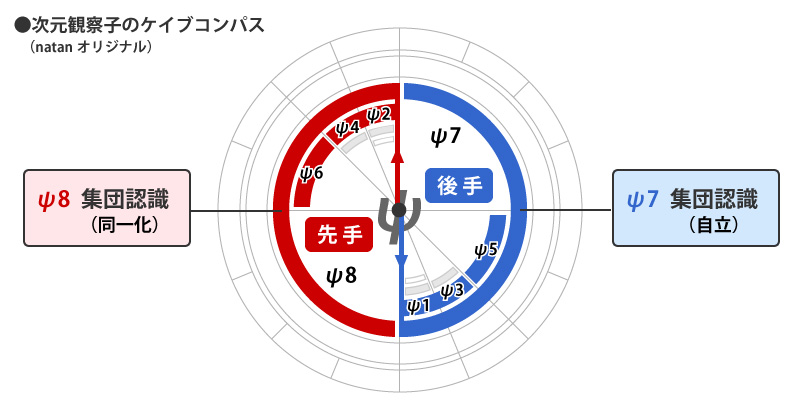
これまでの観察子より、領域が大きいですよね。
私がこれまで使ってきた意識活動の表だと、ψ1~8まで、各観察子の序列だけを見る形になっていますが、本来観察子は「負荷・反映・等化・中和」をくり返して次元上昇していくので、下次元の観察子をすべて含む形で大きくなっていきます。
この下次元をすべて含む形で大きくなっていく様子を、ケイブコンパスなら端的に表現できてしまう、というところがすごいなと思います。
ψ10~9
さらに針を進めると、ψ10~9はこうなります。
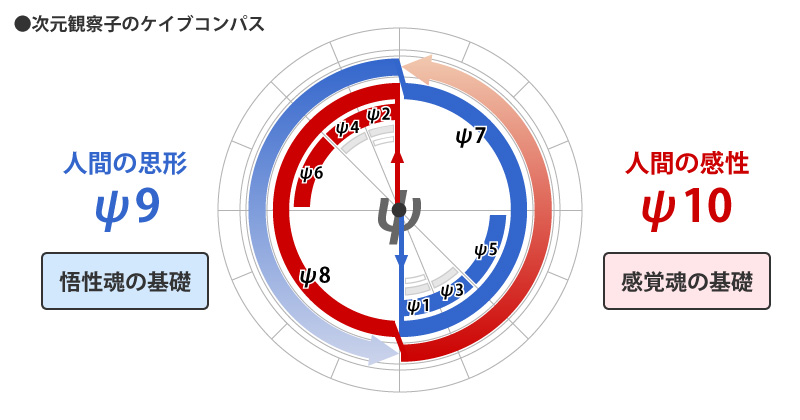
この領域は、ケイブコンパスを見たかぎりだと、ψ10とψ9が180度回転(半回転)しかしていないように見えますが、本当はこの領域はψ10とψ9がともに重なっています。
意識活動の表でもψ10とψ9が重なっているのをイメージして作っているのですが、なんとなくご理解いただけたら嬉しいです(笑)

そしてさらに、この領域は「魂が活動する領域」でもあるので、このように見ることもできます。
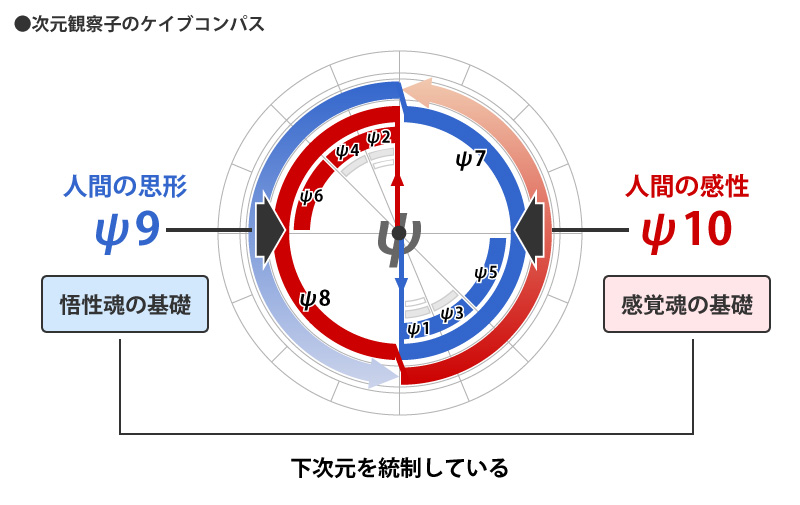
魂が下次元を統制している様子がわかりますね。

今はそれくらいシンプルな理解度で大丈夫です。
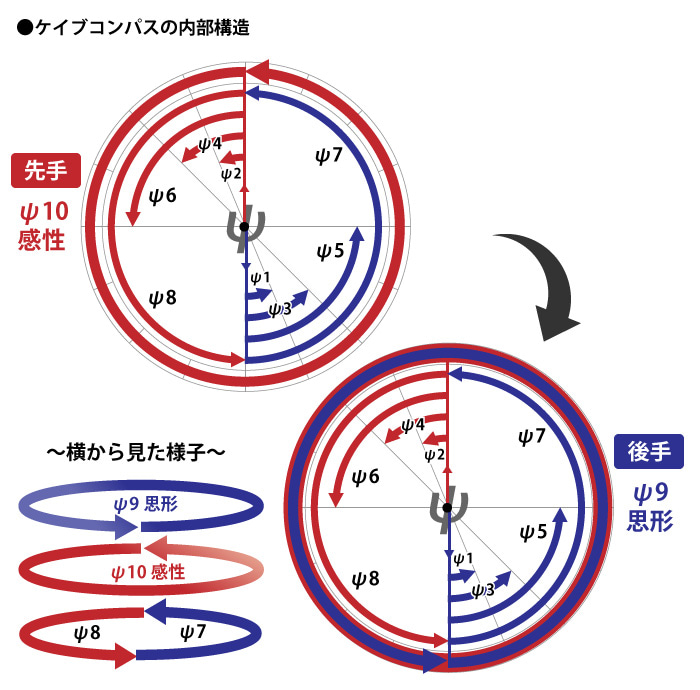
【補足情報】ケイブコンパスの内部構造
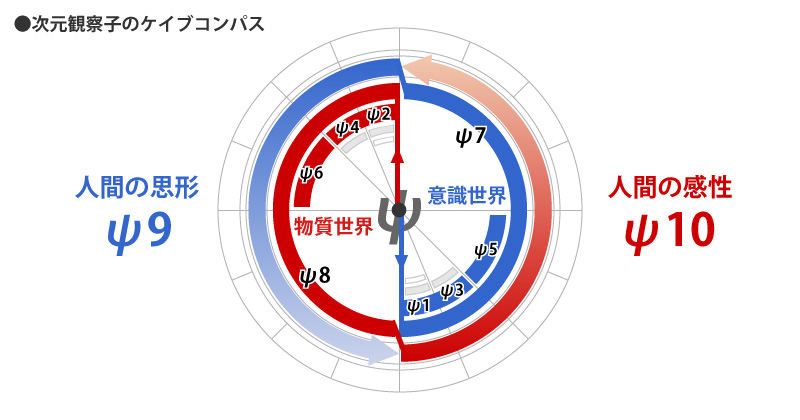
わかりやすいように、ケイブコンパスの内部構造の図を作ってみました。
各観察子の「等化・中和」の状態も、わかりやすく表記しています。
偶数先手でψ8まで進んだら、ψ10(感性)が360度回転して、下次元の全観察子に覆いかぶってきます。
その後、ψ9(思形)が同じく360度回転して、ψ10以下の全観察子に覆いかぶってくる感じです。
多目的に使えるケイブコンパス
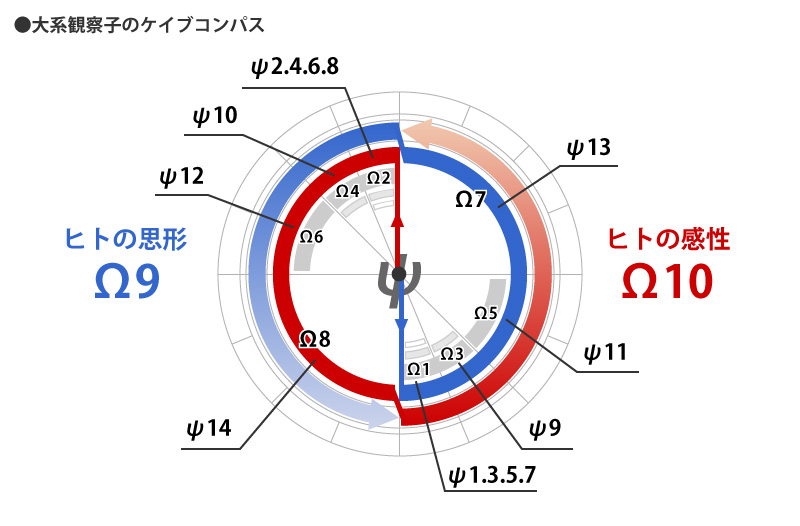
ケイブコンパスは次元観察子だけでなく、上位の大系観察子、脈性観察子でも同様に使用できます。

人類の進化において、各領域で「人間」という言葉の表現が変わっていきます。
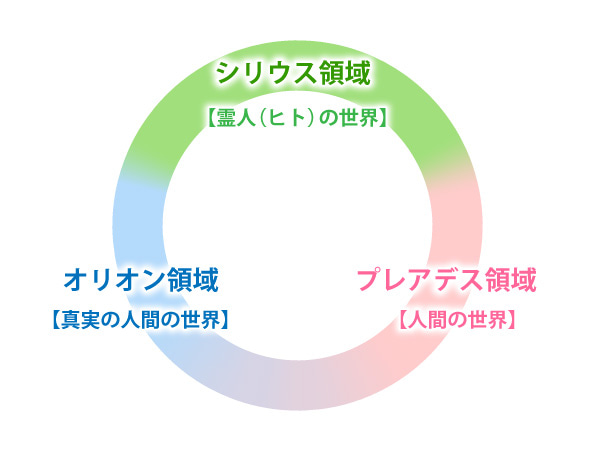
また、一つのコンパスで、複数の領域を見ることもできるので大変便利です。
【動画】本家ヌーソロジーのケイブコンパス解説
Φ=WHY?さんのケイブコンパス解説
ヌーソロジー初心者向けに。cave compass(ケイブコンパス)上での次元観察子の運動は、まず、円の中心にある「重心」から180度真逆になるように,それぞれ円周上の1点ずつに出ることでスタートとなる(つまり、それぞれに起点となるこの2点は180度離れている)。
その片方の点を起点にして、青の流れで、ψ1が22.5度の回転、ψ3が45度の回転、、ψ5が90度の回転、ψ7が:180度の回転(半回転)、ψ9が360度の回転(1回転)、ψ11が720度の回転(2回転)、ψ13が1440度(4回転)。以上が、青の奇数観察子の運動。
もう片方の点を起点にして、赤の流れで、ψ2が22.5度の回転、ψ4が45度の回転、、ψ6が90度の回転、ψ8が:180度の回転(半回転)、ψ10が360度の回転(1回転)、ψ12が720度の回転(2回転)、ψ14が1440度(4回転)。以上が、赤の偶数観察子の運動。
要するに、奇数観察子側は、ψ1:22.5度→ψ3:45度→ψ5:90度→ψ7:180度→ψ9:360度→ψ11:720度→ψ13:1,440度と倍々ゲームになる。偶数観察子側も同様の発展構造を持つ。
このcave compassモデルが特徴的なのは、青の流れがψ7まで進んだ後、ψ9の後半となる次の180度分が、既に赤の流れとしてψ2→ψ4→ψ6→ψ8と進んでいるその上に被ってくるところだ。赤の流れの方も同様。この幾何学モデルで説明される「思形」(ψ9)と「感性」(ψ10)が大きな意味を持つ。
Φ=WHY?(@whyanywhere)
まとめ
ケイブコンパスができる前は、書籍『2013:人類が神を見る日』『2013:シリウス革命』では、最初このようなタカヒマラプレート・チャートが主流だったと思います。
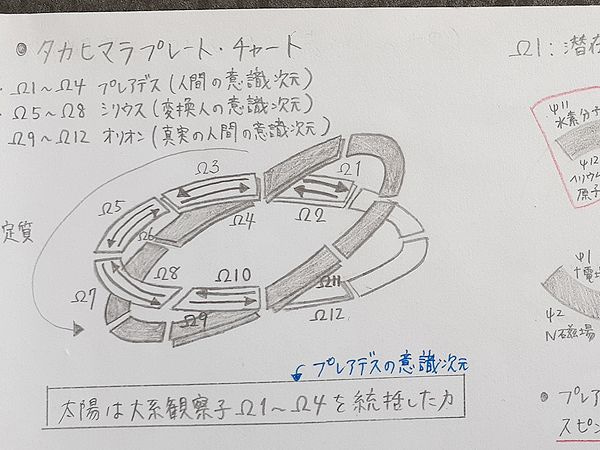

私は何度もノートに描いていたので、フリーハンドで結構上手に書けるようになりました(笑)
でも途中から面倒くさくなって、こう進化しました↓


超手抜き!(笑)
半田さんがOCOT情報を読み解く中で、どんどん進化していったんだと思います。
素晴らしいですね!
▼ 参考文献 ▼
▼ 参考文献 ▼
私が最初ケイブコンパスを見たときは、まだ自分自身が円環状の世界観に慣れていなかったので、ケイブコンパスを理解するのに苦戦しました。
私は女性で、なおかつ方向音痴でもあるので、ケイブコンパスを最初見たとき、どう捉えればよいかわからず頭ごとくるり!と回してしまいました。
あのマリオカートをやると、身体が動いちゃうやつに似ています(笑)
その経験があったので、このブログでは最初に直線上で観察子を表現し、その世界観を理解した後、ケイブコンパスのような円環状の世界に歩みを進めた方がいいなと思い、ようやく今日記事になりました。
もしまだ円環状の世界観に慣れていない方がいらっしゃれば、無理をせず、直線上の世界観で学んでいただいてもOKです。
円環状の世界は、慣れるのに時間がかかりますので。
というわけで、今日はケイブコンパスのお話でした♪
次回もお楽しみに♪