私の宇宙からこんにちは、natanです。
読者さんからいただいたご質問に回答するコーナーです。
広宣さんの本に林檎をひっくり返してく？ワークがあったと思うのですが、もしよかったら、もう少しわかりやすく説明していただけたら嬉しいです。
もう10年以上前からやってるんですが笑
いまいちピンとこないんですが、わかりたいんです(^o^)
2013人類が神を見る日のp370のイメージトレーニングです。
ご質問ありがとうございます♪
このリンゴのワークは、書籍『2013：人類が神を見る日 アドバンストエディション』に書かれているものです。
『2013：人類が神を見る日』のオオムガイの表紙のものは私も持っているのですが、アドバンストエディションは持っていないので、Φ＝WHY？さんから情報提供いただきました。
以下の解説は、本家ヌーソロジーの内容を私流に解釈したものです。本家ヌーソロジーの解説とは異なりますので、ご理解のほどよろしくお願いします。
書籍掲載のワークの内容
ワークは下記内容です。
リンゴでも、コーヒーカップでも、口紅でも何でもいい（できれば球状のものがベスト）。
一つの対象を見つめながら、その周囲に広がっている球空間を使ってこのイメージトレーニング（（注）＜膨張－収縮＞のトレーニングのこと）を何度もやっていると、読者もやがて不思議な感覚に襲われてくるのではないかと思う。
それは、例えば、リンゴの内側に想像されている球空間と、リンゴを包み込んでいる外側の球空間とが互いに反転しているように感じられてくることだ。
つまり、リンゴの方は今まで通りの3次元的な嵩張りを持った球体に見えるのだが、それを取り囲んでいる背景の空間の方は、リンゴを象っている球空間が単純に膨れ上がってできている空間（ψ1）というよりも、リンゴを象っている空間が縮んでいって、それが反転し、リンゴの背景空間となる場所まで膨らんできている空間のように見えてくるということだ。
もし、そう見えない人は、何とかそう見えるようにトレーニングを重ねて欲しい。
一度、その感覚に慣れ親しんでしまうと、どう考えてもそちらの方が心理的に自然な空間認識のように感じてくる。
2013：人類が神を見る日 アドバンストエディションp.371～372より
上記を簡単に説明すると、リンゴの内部空間（ψ1～2）と外部の空間（ψ3～4）を、ψ1～2の膨張収縮の動きを使って見る練習です。
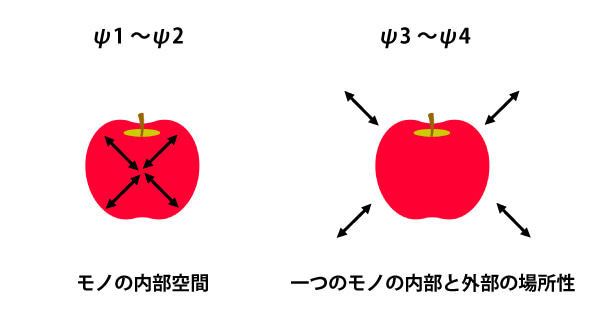
私たちは、モノの外部空間を「モノと背景を別物として」認識しています。
しかし、膨張・収縮でそれぞれの空間が反転するイメージをくり返していると、リンゴの外部空間は空間内にリンゴがポツンと独立して存在しているのではなく、
リンゴと背景が一緒になっている
という感覚が湧いてくるよ、という話だと思われます。
このワークは、「反転」という意味をしっかり理解できていないと難しいと感じます。
ですので、今日はこのワークの解説を通して、しっかり反転を理解できるように徹底解説してみたいと思います。
回答（natan流解説）
リンゴの内部は無限空間
では、まずはじめに、リンゴの内部空間からイメージしてみましょう。
私たちはリンゴの内部空間と聞いても、それより上の次元からリンゴを観察しているので、内部空間は有限の世界だと思っています。
しかし、本当は内部空間は入ってしまえば有限ではなく、無限空間なのです。
そう簡単には出られません。
この無限空間から出て、一つ上の次元に出るために
反転
というものが必要になってくるのです。
反転とは以前もお話しましたが、宇宙空間を例にすると、ロケットに乗って光速度で空間内を突っ切ると、空間内がローレンツ収縮を起こして、ミクロの世界に入っていくことでグレン！と空間が反転する現象のことです。
宇宙空間が「点」へ収縮することでグレン！
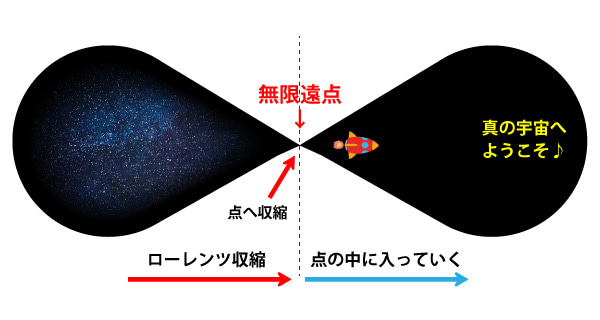
このローレンツ収縮を起こして点へ収縮し、無限遠点を超えて膨張＆反転が起こることで、真の宇宙へ出る様子を、リンゴの内部空間に当てはめて思考していきます。
【思考実験】①リンゴの内部空間
イラストで上記の様子を表現したらカッコ良かったのかもしれませんが、私はイラストが描けないもので…。
久しぶりにDIYしましたよ（笑）
こちらがリンゴの内部空間です↓
内部空間だと思ってください（汗）
表現とクオリティに限界があるのだ！！（笑）
本当は、球空間で表現するのがベストだと思いますが、表現が難しいため2次元平面で見ていきます。
【思考実験】②収縮
では早速、この内部空間から一つ上の次元に出ます。
上位の次元に出るためには、まずは収縮！
これ、ローレンツ収縮だと思ってください（笑）
フェルト生地を穴に通さなければいけないので、結構大きめの穴を作ったのですが、本当は素粒子レベルのミクロサイズの穴、もしくは点へ収縮していると思ってみてください。
【思考実験】③膨張
この収縮する様子を横から見てみると、下記のような感じになっています。
リンゴの内部空間が収縮することで、今度は裏側から何かが膨張してきましたね。
膨張しているものを、真正面から見てみましょう。
おっと！何やら変なもの出てきました！！
これを別角度から、もう一度見てみます。
おぉ～っと！
リンゴの外部空間らしきものが出てきた～!!
2次元平面なので、正確に膨張を再現すると、リンゴの中央部が膨張して出現するというよりは、空間の端？から広がっていくのかもしれません。
細かすぎるかな？
細かすぎて伝わらないヌーソロジー選手権（笑）
空間が膨張して出てくるイメージは、下記動画のようなイメージだと思ってみてください。
【思考実験】④リンゴの外部空間の出現
そして、さらに収縮→膨張が進むと…、ジャーン！！！
リンゴの外部空間（ψ3～4）が出現しました！！
反転が起こることで、今度はリンゴの内部空間（ψ1～2）が見えなくなりました！
下手なDIYでスミマセン…。
反転のおさらい
つまり、反転とは「裏表が逆になること」なんですが、ヌーソロジーの空間構造で反転を思考するときは、
という意味だと思ってください。
そして、その反転が起こることで次元上昇します。
リンゴの内部空間（ψ1～2）にいるときは、そこは無限空間になっているので、外部の空間は知覚できません。
しかし、裏の見えない世界には、ちゃんとリンゴの外部空間（ψ3～4）が存在しているのです。
その裏の世界こそが、一つ上の次元になっています。
これが本家ヌーソロジーでは、下記のように描写されます。
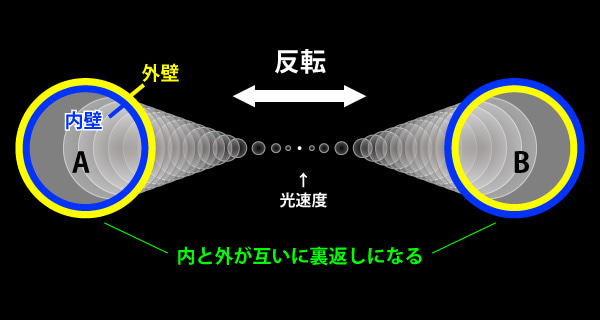
「反転」に対する誤った認識
私たち人間にとって、「反転」という言葉の概念は、ウラとオモテが同じ次元の中で見え隠れしているだけというイメージで捉えているかと思います。
ですので「ウラとオモテをひっくり返すことを反転という」と説明を聞いても、そこに次元上昇が絡んでいるとは一切思いません。
私も今回はフェルト生地を使って説明しているので、どうやってみても同じ次元内でのウラとオモテの話だと思ってしまいます。
ですが実際、このウラとオモテは「空間」に関することなので、今まで見えなかった空間が反転によって出現するということは、まったく違う世界が出現することなので、次元上昇もしくは次元に変化が出ていることになるのです。
また、私たち人間の意識は、モノの内部に閉じ込められています。
そのため、リンゴの内部から外部に出ても、リンゴはさらに上位の空間内にポツーンと独立して存在していると思っています。
なので「リンゴの内部から外部に出る」と聞いて、下記のようにリンゴの外部にポーン！と出るイメージを私たちは想像してしまいがちです。
上記イメージを持っていることこそが、「意識がモノの内部に落ち込んでいる」というなによりの証拠です。
じつはそうではなく、空間における本当の次元上昇とは、反転によって起こるものなのです。
そして、リンゴの外部空間とは下記画像のように、ムクムクムクッ！とリンゴと背景がセットになって出現しているのです。
なので、モノと背景がセットになって出現しているのだから、この次元内に私たち人間が存在できるはずがないのです。
私たちはもっと、上位の次元からその世界を見ています。
モノと背景の次元は、2次元射影の世界です。
この、膨張して背景とリンゴがセットになって出てくる様子。
このようなイメージで空間を思考すると、認識に変化が出てくるよというのがリンゴのワークが言わんとすることだと思われます。
これを膨張・収縮、そしてヌーソロジーでいう反転の意味として、私なりに表現してみた次第です。
まとめ
いかがでしたでしょうか？
反転の意味が理解できそうですか？
それぞれの空間を膨張・収縮で捉えるとき、空間が呼吸している、もしくは生きているかのように膨らんではしぼんで～という、滑らかな動きでイメージをくり返すとよいかもしれません。
何度も何度もイメージトレーニングを行って、反転の意味を腑に落としてくださいね♪
ご質問ありがとうございました！
最後に一つだけ。
リンゴの内部空間を赤いフェルトで作ったけど…、
リンゴの内部って赤いか!?
という疑問が沸いて、一人で笑っちゃった（笑）
以上です♪
コメント